las ecuaciones

Las ecuaciones 

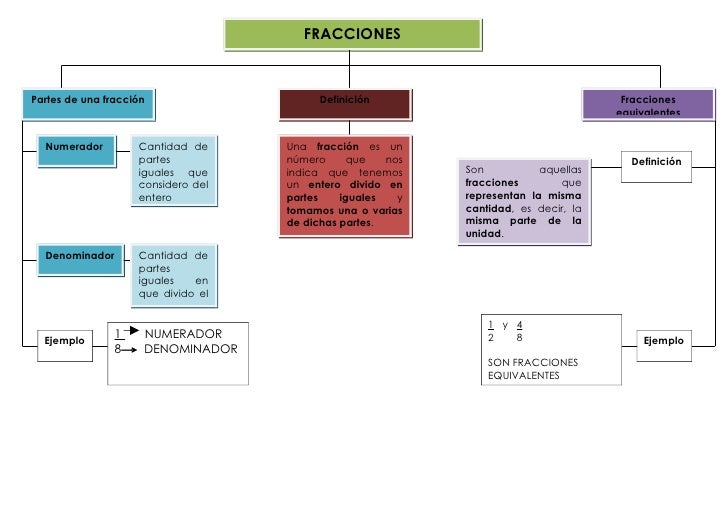
En matemática se llama ecuación a la igualdad de dos expresiones algebraicas, que serán denominados miembros de la ecuación y separadas por el signo igual. En la ecuaciones, aparecerán relacionados a través de operaciones matemáticas, números y letras (incógnitas). Los datos por lo general se encuentran representados  por coeficientes, variables, números y constantes, mientras que las incógnitas presentan las letras y representan el valor que se quiere descifrar a través de la ecuación. 

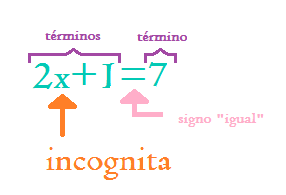
la igualdad planteada por una ecuación sera cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables (incógnitas) la hacen cierta.

las ecuaciones sirven básicamente, para resolver cualquier tipo de problemas, ya sean matemáticos de la vida diaria o en cualquier rama de la ciencia.

Historia de las ecuaciones

La civilización egipcia fue una de las primeras en utilizar ecuaciones matemáticas, pues para el siglo XVI ya aplicaban dicho sistema, para resolver problema asociados con la repartición de alimentos, aunque no eran llamados ecuaciones, se podría decir que es el equivalente a la época actual. también los chinos poseían conocimientos de tale soluciones matemáticas, pues para principios de la era escribieron un libro donde se planteaban diversos métodos para la resolución de ecuaciones de segundo grado y primer grado.

Durante la edad media las ecuaciones matemáticas tuvieron un gran impulso, pues estas eran utilizadas como desafíos públicos entre los expertos de la época. Para el siglo XVI dos importantes matemáticos realizaron el descubrimiento de utilizar los números imaginarios para poder solucionar ecuaciones de segundo, tercero y cuarto grado. también en ese siglo Rene Descartes hizo famosa la notación científica, ademas de ello, en ese siglo se hizo publico también uno de los teoremas mas populares de la matemática ''El ultimo teorema de Fermat''. Durante el siglo XVII los científicos Gottfried Leibniz e Isaac Newton  hicieron posible la solución de las ecuaciones diferenciales, lo que dio origen a una serie de descubrimientos que se dieron durante esa época con respecto a esas ecuaciones en especifico.

  

Gottfried Leibniz         Isaac Newton

Tipos de ecuaciones:

Ejemplo de los tipos de ecuaciones;

Las Fracciones

Los números fraccionario 

Los números fraccionario se encuentran dentro del conjuntos de los números racionales.Surgen por las necesidad de dar solución a la división en el conjuntos de los números naturales. 

   

Los números fraccionarios comunes se forman al plantear una división entre dos números naturales, teniendo en cuenta que siempre el divisor debe ser diferente de cero.

En un numero fraccionario, el denominador indica la partes en que se divide la unidad y el numerador. Formas de expresión de una fracción puede considerarse como el cociente exacto de dividir el numerador con el denominador, de ahí que se puede escribir también como el cociente a:b.

Una fracción representa un numero natural cuando al dividir el numerador con el denominador el resto de la división es cero.

Las fracciones comunes se pueden expresar en notación decimal . El numero que se encuentran a la izquierda de la coma es la parte entera y las cifras que quedan situada a la derecha de la coma es la parte decimal. La primera cifra después de la coma representa las décimas, la segunda la centésimas .

esquema de los números fraccionarios

Los números imaginarios

Los números imaginarios

Los números imaginarios pueden expresarse como el producto de un número real por la unidad imaginaria i, en donde la letra i denota la raíz cuadrada de -1, es decir;

Z=Yi

En álgebra particularmente, un número imaginario es un número complejo, cuya parte real es igual a cero, ejemplo 3i es un número imaginario, al igual que i y -i que son números imaginarios.

                                      

       

El género de los números complejos/imaginarios lo inventó Raffaelle Bombelli un matemático e ingeniero italiano en el siglo XVI. El término de número imaginario fue creado por René Descartes, en su tratado geometría, en oposición a la teoría de Bombelli.

                

Raffaelle Bombelli         Rene descartes

En el año 1777 cuando Leonhard Euler le dio a la raíz de -1 el nombre de i, por imaginario, de manera despectiva dando a entender que no tenía una existencia real.

Leonhard Euler

Introducción a los números imaginarios: